Solution: Left-truncated survival times

a)

In general we have

\[S(t) = \exp(-A(t)) = \exp\left(-\int_0^t \alpha(s) ds \right)\]

For \(t> v\):

\begin{align*} S(t\mid v) &= P(T>t\mid T>v) = \frac{P(T>t\cap T>v)}{P(T>v)} \\ &=\frac{P(T>t)}{P(T>v)} \\ & = \frac{\exp(-\int_0^t \alpha(s) ds)}{\exp(-\int_0^v \alpha(s) ds)}\\ &= \exp\left(-\left[\int_0^t \alpha(s) ds - \int_0^v \alpha(s) ds\right]\right) \\ &= \exp\left(-\int_v^t \alpha(s) ds\right) \end{align*}

For \(t\leq v\) we clearly must have

\[ S(t\mid v) = P(T>t\mid T>v) = 1. \]

Next we want to find the hazard rate \( \alpha (t\mid v) = -\frac{d}{dt} \ln S(t\mid v)\).

For \(t\leq v\):

\[\alpha (t\mid v) = -\frac{d}{dt} \ln 1 = 0.\]

For \(t> v\):

\begin{align*} \alpha (t\mid v) &= -\frac{d}{dt} \ln \left[\exp\left(-\int_v^t \alpha(s) ds\right)\right] \\ &= -\frac{d}{dt} \left(-\int_v^t\alpha(s) ds\right) \\ &= \alpha(t). \end{align*}

So

\[ \alpha( t\mid v) = \begin{cases} 0 & \text{for } t\leq v \\ \alpha(t) & \text{ for } t> v\end{cases}\]

b)

We let \( 0<v<u \), and consider the left-truncated and right-censored survival time \( \widetilde{T} = \min\{T, u\} \), and let \( D = I(\widetilde{T} = T) \). We want to find the intensity process of the counting process \( N(t) = I(v < \widetilde{T} \leq t, \quad D = 1) \).

We have that \( \lambda(t) dt = P(dN(t) = 1\mid \mathcal{F}_{t-}) \).

\[ dN(t) = \begin{cases} 0 & \text{for } t\leq v \\ I(t\leq T< t+dt) \\ 0 & \text{for } t > u. \end{cases}\]

So clearly we have \( \lambda(t) = 0\) for \(t\leq v\) and for \(t > u\).

For \( t \in (v, u] \) we get

\begin{align*} \lambda(t) dt &= P(t \leq T < t+dt \mid T> v, \mathcal{F}_{t-}) \\ & = \begin{cases}0 & \text{if } T< t \\ P(t \leq T < t+dt \mid T\geq t) & \text{if } T\geq t\end{cases} \\ & = \alpha(t) dt \cdot I(T \geq t) \end{align*}

So we get

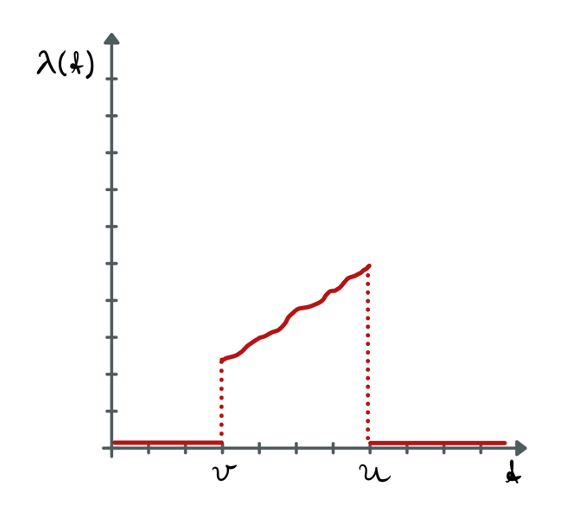
\[ \lambda(t) = \begin{cases} \alpha(t) \cdot I(T \geq t) & \text{for } t\in(v, u] \\ 0 & \text{otherwise.} \end{cases} \]

What might a sample path look like?