Solution: Survival function and hazard rate for the exponential distribution
Eksempel
We start by finding the survival function \(S(t)\) from the given density \(f(t),\) and thereafter find the hazard rate \(\alpha(t)\) from the survial function \(S(t).\)
Survival function
The survival function \(S(t)\) is defined as \[S(t)=P(T>t).\] The survival function can therefore clearly be found by integrating the density function. For \(t>0\) we have \begin{align*}S(t) &= P(T>t)\\ &= \int_t^\infty f(s) ds\\ &= \int_t^\infty \lambda e^{-\lambda s} ds\\ &= \left[ - e^{-\lambda s}\right]_{s=t}^{\infty}\\ &= 0 - \left( - e^{-\lambda t}\right)\\ &= e^{-\lambda t}.\end{align*} Thus, the survival function for the exponential distribution is \[\underline{\underline{S(t)=e^{-\lambda t},t>0.}}\]
Hazard rate
The hazard rate \(\alpha (t)\) is given from the survival function \(S(t)\) by \[\alpha(t)=- \frac{d}{dt}\left[\ln S(t)\right].\] When the survival function is as given above we get \[\ln S(t) = -\lambda t,\] which in turn gives \begin{align*}\alpha(t) &= - \frac{d}{dt}\left[ -\lambda t\right]\\ &= \lambda.\end{align*} Thus, the hazard rate for the exponential distribution is a constant function, \[\underline{\underline{\alpha(t) = \lambda, t>0.}}\]
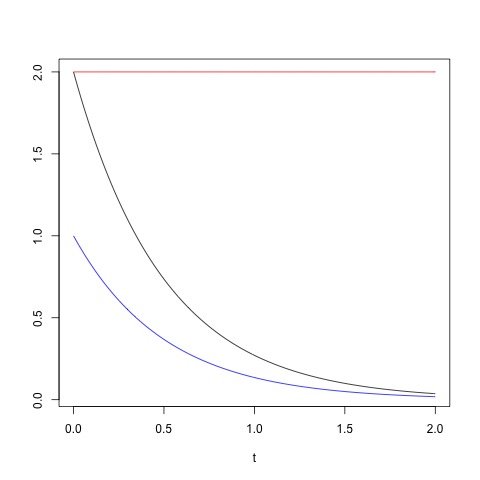
Plots of \(f(t),\) \(S(t)\) and \(\alpha(t)\) for \(\lambda=2.0\)
The R code in Code 1 can be used to plot the density function, survival function and the hazard rate when \(\lambda=2.0\) on the interval \(t\in (0,2).\)
lambda = 2.0
t = seq(0,2,0.01)
plot(t,lambda*exp(-lambda * t),col="black",xlab="t",ylab="",type="l")
lines(t,exp(-lambda * t),col="blue",type="l")
lines(t,lambda * rep(1,length(t)),col="red",type="l")
Figure 1 shows the plot that is produced by running the R code in Code 1.